Persamaan linear adalah sebuah persamaan aljabar, yang tiap
sukunya mengandung konstanta, atau perkalian konstanta dengan variabel tunggal.
Persamaan ini dikatakan linear sebab hubungan matematis ini dapat digambarkan
sebagai garis lurus dalam Sistem koordinat Kartesius.
Contoh grafik dari suatu persamaan linear dengan nilai m=0,5
dan b=2 (garis merah)
Bentuk umum untuk persamaan linear adalah
Dalam
hal ini, konstanta m akan menggambarkan gradien garis, dan konstanta b merupakan
titik potong garis dengan sumbu-y. Persamaan lain, seperti x3, y1/2, dan xy bukanlah
persamaan linear.
Contoh sistem persamaan linear dua variabel:
Sistem Persamaan Linear Dua Variabel
Persamaan linear yang rumit, seperti di sebut di atas, bisa
ditulis dengan menggunakan hukum aljabar agar menjadi bentuk yang lebih
sederhana. Seperti contoh, huruf besar di persamaan merupakan konstanta, dan x
dan y adalah variabelnya.
Bentuk Umum
dimana
konstanta A dan B bila dijumlahkan, hasilnya bukan angka nol. Konstanta
dituliskan sebagai A ≥ 0, seperti yang telah disepakati
ahli matematika bahwa konstanta tidak boleh sama dengan nol. Grafik persamaan
ini bila digambarkan, akan menghasilkan sebuah garis lurus dan setiap garis
dituliskan dalam sebuah persamaan seperti yang tertera diatas. Bila A ≥
0, dan x sebagai titik potong, maka titik koordinat-xadalah ketika garis bersilangan dengan sumbu-x (y = 0) yang digambarkan dengan rumus -c/a. Bila B≥ 0, dan y sebagai
titik potong, maka titik koordinat- y adalah ketika garis bersilangan
dengan sumbu-y (x =
0), yang digambarkan dengan rumus -c/b.
Bentuk standar
di mana, a dan b jika dijumlahkan, tidak menghasilkan angka
nol dan a bukanlah angka negatif. Bentuk standar ini dapat diubah ke bentuk
umum, tapi tidak bisa diubah ke semua bentuk, apabila a dan b adalah nol.
Bentuk titik potong gradien
Sumbu-y
dimana m merupakan gradien dari garis persamaan, dan titik
koordinat y adalah persilangan dari sumbu-y. Ini dapat digambarkan dengan x =
0, yang memberikan nilai y = b. Persamaan ini digunakan untuk mencari sumbu-y,
dimana telah diketahui nilai dari x. Y dalam rumus tersebut merupakan koordinat
y yang anda taruh di grafik. Sedangkan X merupakan koordinat x yang anda taruh
di grafik.
Sumbu-x
dimana m merupakan
gradien dari garis persamaan, dan c adalah titik potong-x,
dan titik koordinat x adalah persilangan dari sumbu-x.
Ini dapat digambarkan dengan y = 0, yang memberikan nilai x = c. Bentuk y/m dalam persamaan sendiri berarti bahwa
membalikkan gradien dan mengalikannya dengan y. Persamaan ini tidak mencari titik
koordinat x, dimana nilai y sudah diberikan.
Sistem persamaan linear lebih dari dua variabel
Sebuah persamaan linear bisa mempunyai lebih dari dua
variabel, seperti berikut ini:
di mana dalam bentuk ini, digambarkan
bahwa a1 adalah koefisien untuk variabel pertama, x1, dan n merupakan jumlah
variabel total, serta b adalah konstanta.



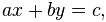


0 Komentar untuk "Contoh Persamaan Linear dan Pengertiannya"